Derivadas de Orden superior

 Derivadas de Orden superior


Es encontrar las derivadas según su orden según lo pida el ejercicio. 








DERIVADAS DE ORDEN SUPERIOR



Las derivadas de orden superior se obtienen al derivar una función y = f (x), tantas veces como lo indique el orden requerido.
  • La derivada de una función se llama primera derivada y se denota con
  • La derivada de la derivada se llama segunda derivada y se denota con
  • El proceso de hallar derivadas, una tras otra, se llama derivadas sucesivas.
  • La enésima derivada de una función se denota con

Si derivamos la derivada de una función, derivada primera, obtenemos una nueva función que se llama derivada segunda, f ' '(x). Si volvemos a derivar obtenemos la derivada tercera, f ' ' '(x). Si derivamos otra vez obtenemos la cuarta derivada f ' ' ' ' y así sucesivamente.


EJEMPLO N° 1
Obtenga la Tercera derivada de la función f(x) = 2x3 + 4x2 – 5x + 1

PASO N° 1
Se obtiene la primera derivada de la función:




PASO N° 2
Se obtiene la segunda derivada de la función:



PASO N° 3
Se obtiene la segunda derivada de la función:




EJEMPLO N° 2
Obtenga la segunda derivada de la función

PASO N° 1
Se obtiene la primera derivada de la función:



PASO N° 2
Se obtiene la segunda derivada de la función:





EJEMPLO N° 3
Obtenga la segunda derivada de la función

PASO N° 1
Se obtiene la primera derivada de la función:





PASO N° 2
Se obtiene la segunda derivada de la función:






DERIVADAS DE ORDEN SUPERIOR. (s/f). Blogspot.com. Recuperado el 26 de julio de 2024, de https://drepasovirtual.blogspot.com/p/derivadas-de-orden-superior.html




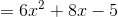
Comentarios

Publicar un comentario

Entradas más populares de este blog

Teorema de limites

Imagen
TEOREMA DE LIMITES  En este tema nos explico el profe como encontrar el limite de una función f(x),es el punto x el cual el valor se  acerca a los valores de y, de un principio no entendía muy bien ese tema de lo de algebra se me dificulto un poco pero me fue útil la explicación del profe  de buscar el resultado si te sale indeterminado en el resultado, por otra parte la factorización aun se me complica en cuanto a los signos de + y de - menos es lo que vengo repasando en estos días para comprender aun mas este tema, e estado viendo videos como nos los sugirió el profe un poco de todos los temas para comprender mas.
Leer más

Limites por Racionalización

Imagen
 Limites por racionalización  es cuando esta una raíz en el numerador o en el denominador para esto se multiplican por su conjugado, cuándo se conjuga solo se cambia el signo. Calculo de limites usando Racionalización Publicado el  20 noviembre, 2017 Este tipo de limites se presenta cuando aparece una raíz en el numerador o el denominador de  una función racion al y está al ser evaluado el limite se vuelve cero en el denominador. Racionalizar una fracción consiste en conseguir que su denominador sea racional y , podemos considerarlo como un proceso de simplificación.       Para estos limites tenemos que tener en cuenta lo siguiente: Conjugado de un termino Es un binomio que se toma con diferente signo entre dos factores. Ejemplo: Para resolver los limites se realiza los siguientes pasos: Se escribe el conjugado del termino que tenga raíz Se multiplica el numerador y el denominador por el conjugado Se realiza las operaciones de ...
Leer más

Reglas de derivación

Imagen
 Reglas de derivación Comprendimos que para derivara tenemos que utilizar diferente tipo de reglas algebraicas para obtener resultados exactos. Se dice que la derivada de una constante es 0 por ejemplo y=2     y'=0 la derivada de la variable x es 1 ejemplo y=x  y'=1 o cuando la derivada x tiene un coeficiente y=5x igual   y'=5 solo se pasa el coeficiente o por ejemplo cuando tenemos y=3x ala 6 solo se multiplica por el exponente y se le resta 1 su derivada seria y'=18x ala 5. Como se habrá notado en el capítulo anterior, para calcular la derivada de una función y D f .x/ mediante la definición, usando la denominada regla de los cuatro pasos, generalmente es necesario llevar a cabo un laborioso procedimiento algebraico. Para evitar tal complejidad, se opta por el uso o la aplicación de resultados o reglas básicas generales que nos permiten el cálculo de la derivada de diversas funciones de uso frecuente. Dichas reglas se demuestran a partir de la defini...
Leer más